Shahram Pezeshk, Ph.D., P.E.
Chair and Professor of Civil Engineering
Engineering Science Building - Room 104A
Department of Civil Engineering
The University of Memphis
Memphis, TN 38152
Phone: (901) 678-4727 (office)
Secretary
: (901) 678-2746 spezeshk@memphis.edu
| Research Areas: |
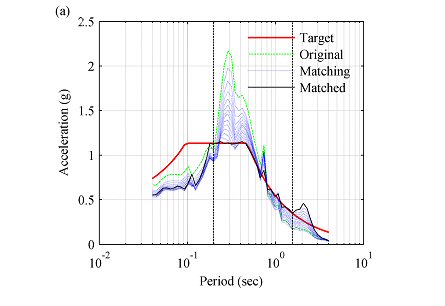
Existing spectral matching techniques in the frequency domain distort the displacement time history of the ground motions. This study shows that the velocity value at the end of the record is not affected by Fourier amplitude spectrum scaling but the displacement may linearly increase (or decrease) boundlessly. Two numerical solutions are proposed to solve the displacement drift problem in the frequency domain. Following the proposed frequency domain base-line correction procedure, one does not need to perform a base-line correction in the time domain after completing the spectral matching. As a result, acceleration, velocity, and displacement time histories will remain fully compatible and the boundary conditions of the velocity and displacement time histories will be preserved. The proposed procedure is not limited to spectrum matching methods and can be used with any general filtering process to retain the final displacement of the record.
The possibility of applying a zero-padding technique to the spectral matching filter is also discussed. It is shown that applying an appropriate window along with the zero-padding technique can lead to a reasonable displacement time history. The proposed procedures can be easily added to existing or new frequency domain spectral matching algorithms without significantly disrupting the spectral matching process.
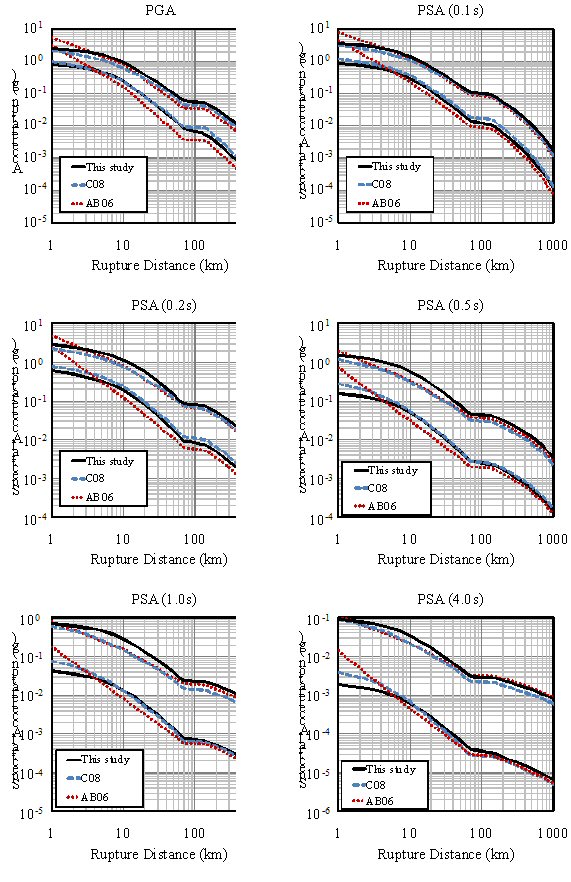
In the field of earthquake engineering, ground-motion prediction models are frequently used to estimate the peak ground motion (PGA) and the pseudo spectral acceleration (PSA). In regions of the world where ground-motion recordings are plentiful (such as WNA), the ground-motion prediction equations are obtained using empirical methods. In other regions such as eastern North America (ENA), with insufficient ground-motion data, other methods must be used to develop ground-motion prediction equations. The hybrid empirical method is one such method used to develop ground-motion prediction equations in areas with sparse ground motion. This method uses the stochastic method to adjust empirical ground-motion prediction relations developed for a region with abundant strong motion recordings. It estimates strong-motion parameters in a region with a sparse database. The adjustments take into account differences in the earthquake source, wave propagation, and site-response characteristics between the two regions. The purpose of this study is to use a hybrid empirical method and to develop a new hybrid empirical ground-motion prediction equation for ENA, using five new ground-motion prediction models developed by the Pacific Earthquake Engineering Research Center (PEER) for WNA. A new functional form is defined for the ground-motion prediction relation for a magnitude range of 5 to 8 and closest distances to the fault rupture up to 1000 km. Ground-motion prediction equations are developed for the response spectra (pseudo-acceleration, 5% damped) and the peak ground acceleration (PGA) for hard-rock sites in ENA. The resulting ground-motion prediction model developed in this study is compared with recent ground-motion prediction relations developed for ENA, as well as with available observed data for ENA.
An automated performance-based design methodology to optimize structural and non-structural system performance is outlined and it is shown that it can be used to enhance understanding of structural steel system design for minimum life-cycle costs. Performance is assessed using loss probability with direct economic loss expressed as a percentage of the building replacement cost. Time-based performance assessment is used to compute the expected annual loss of a given steel framing system assuming exposure to three seismic hazard levels. Damage to the structural system, non-structural displacement-sensitive components, and non-structural acceleration-sensitive components is characterized using fragility functions. A steel building with three-story, four-bay topology taken from the literature is used to demonstrate application of the algorithm with subsequent comparison of designs obtained using the proposed methodology and others found in the literature. 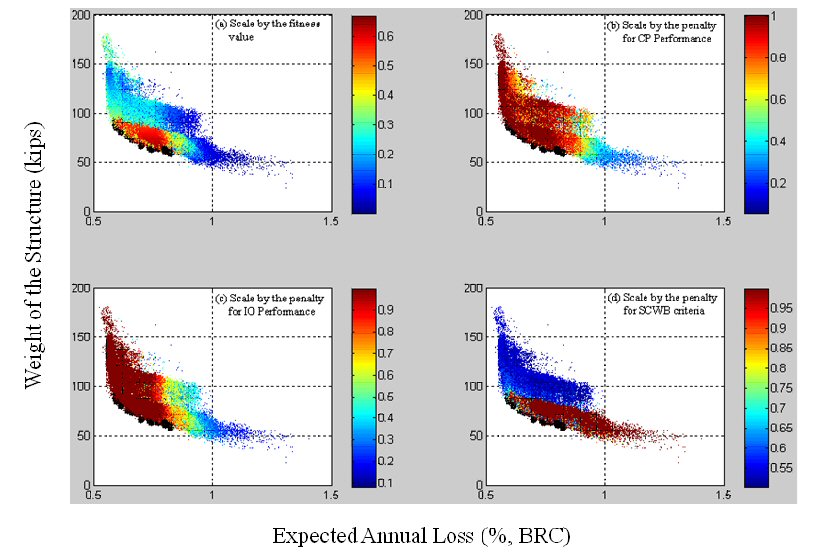
|
Note:Copyright and all rights therein are retained by the authors or copyright holders. All persons using these documents are expected to adhere to the terms and constraints invoked by each author's copyright.
|