"I am always ready to learn, but I do not always like being taught."  Winston Churchill

Part One: Solve the following three problems (you are not required to use an Excel spreadsheet)

Carbon Dioxide Removal #1

• A groundwater containing 30 mg/l of carbon dioxide is to be degasified using a multiple-tray aerator with six trays. In this water treatment facility, ten aerators operating in parallel. For maintenance reasons, only nine of the aerators are available at any one time. The design population is 50,000 persons, and the maximum day demand is 150 gal/person-day. The k value is 0.33, and the hydraulic loading is 3 gpm/ft². Determine:
  

1. The carbon dioxide content of the product water.

2. The size of the trays if the length-to-width ratio is 2:1 and the trays are made to 1 inch increments.

Solution: The performance equation is:

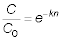
Therefore:  C = (30 mg/l)e^-6(0.33) = (30 mg/l)(0.138) = 4.1 mg/l

The flowrate to each parallel aerator is:

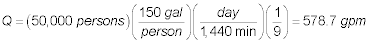
The area of each parallel aeration tray is:

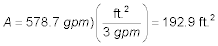
Since L = 2W, then the area of each aerator is A = W(2W) = 192.9 ft²

W = 9.82 ft  or    9 ft - 10 in
L = 2W        or   19 ft -  8 in

Carbon Dioxide Removal #2

• A groundwater containing 25 mg/l of carbon dioxide is to be degasified using a multiple-tray aerator. The design population is 250,000 persons, and the maximum day demand is 150 gal/person-day. The k value is 0.32, and the hydraulic loading is 4 gpm/ft². Determine:
  
  

  1. Determine the total number of trays in an aerator required to reduce the product water's carbon dioxide content by 90%.

  2. Determine the number of aerators, operated in parallel, required for the water treatment facility if each tray's size is 1,000 ft².

Solution: The performance equation is:

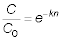
Rewriting the aeration equation to solve for n, the number of trays gives:

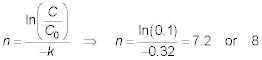
The flowrate to each parallel aerator is:

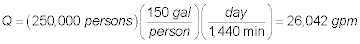
The The total area of all aerations is:

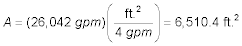
The number of 1,000 ft² aerators is:

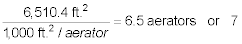
Therefore the number of 1,000 ft² 8-tray aerators required to treat 26,042 gpm is 7.

 Disinfection

• The following is actual data for a virus exposed to an experimental disinfectant. Estimate the contact time required to obtain a reduction of the 1/40,000 of the original number of virus.

Solution: The empirical data for the disinfection model should be plotted with time on the x-axis and ln(N/N₀) on the y-axis. The slope of the line on this plot with give you an estimate of the disinfection constant.

Time, seconds	1	2	4	8
N/N0	4,270/10,000	1,830/10,000	332/10,000	11/10,000
-ln(N/N0)	0.8510	1.6983	3.4052	6.8124

The data are plotted below:

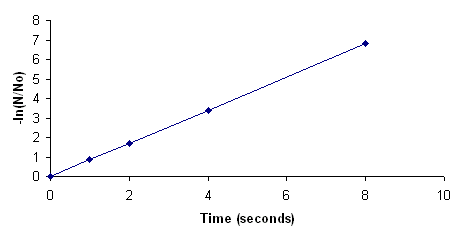
The slope of the line is the disinfection constant.

slope = 6.8124/(8 seconds) = 0.851/sec

The time required for a reduction in cell activity of 1/40,000 is:

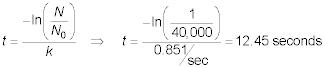
The contact time required to obtain a reduction of the 1/40,000 of the original number of virus is 12.45 seconds.

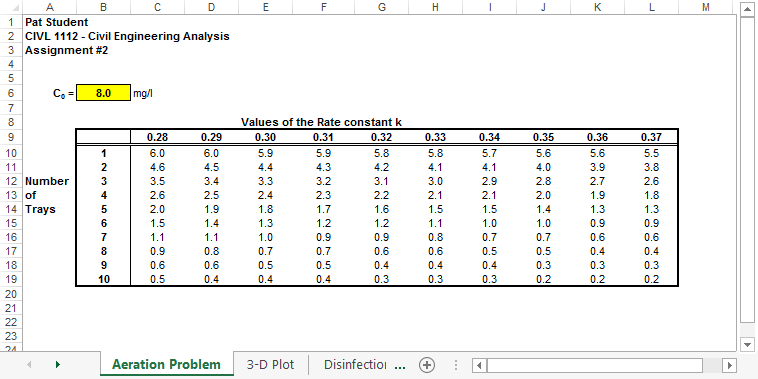
Part 2:  Use Excel to develop a table containing the removal of carbon dioxide in a water treatment process using the aeration model we described in class.