Consider the problem of a classical square vibrating membrane with all edges fixed against transverse displacement. The differential equation of motion can be written as:

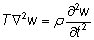
where T is the initial tension in the membrane and ρ the area density. The boundary condition is that w vanishes on all the edges of the membrane. Taking:

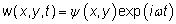
leads to:

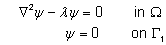
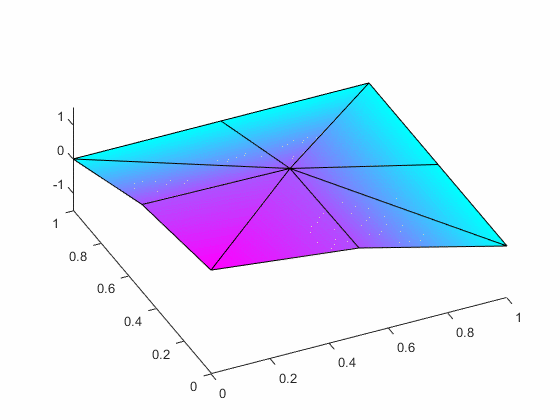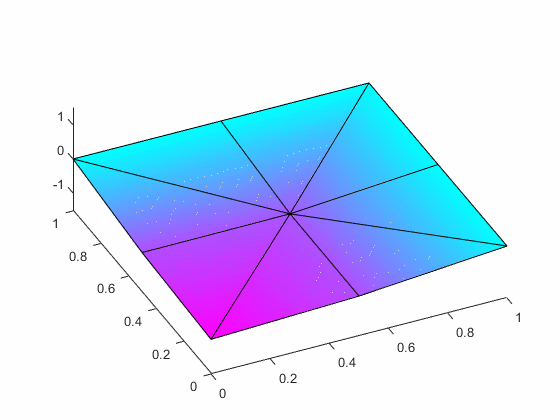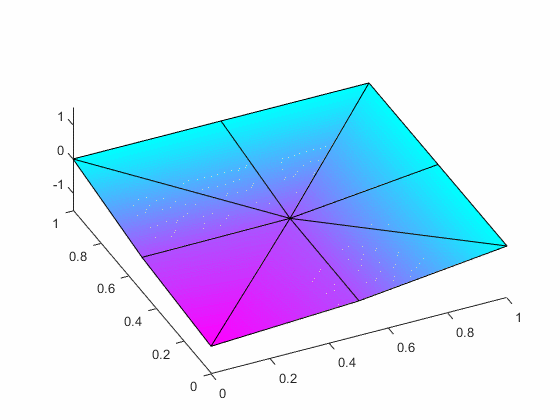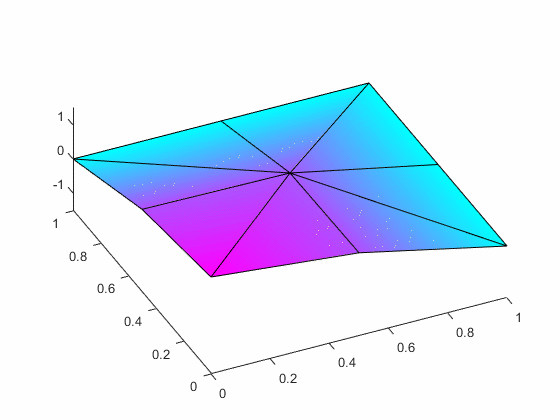
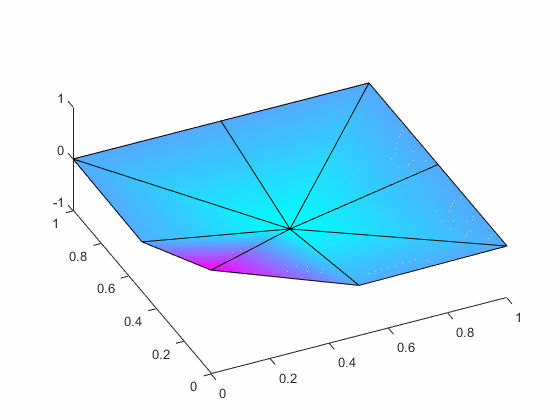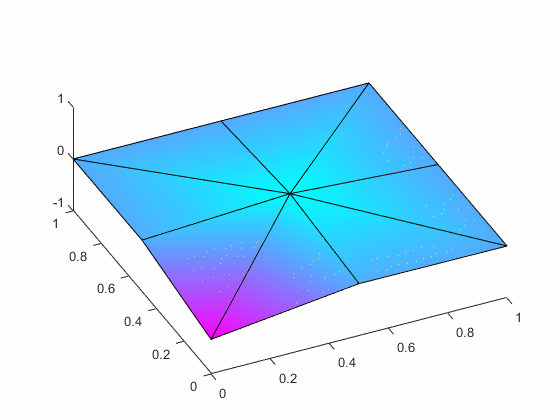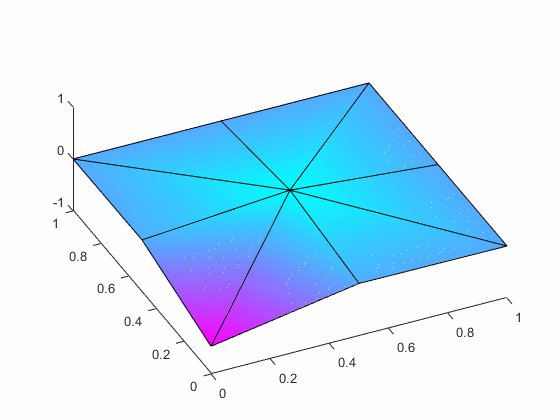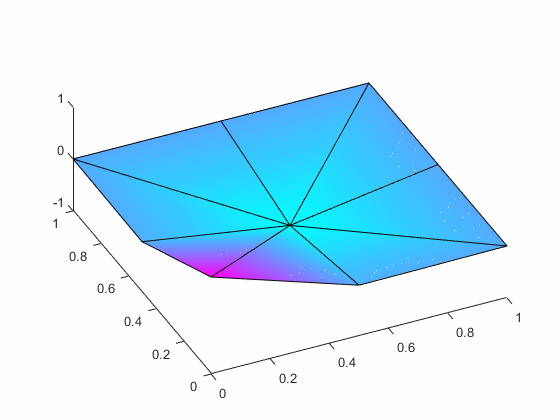
where l = rw²/T. This is the Helmholtz problem on the square, with the dependent variable y prescribed as zero everywhere on the boundary.  Model the top right-most quadrant of the membrane using eight equally-sized 3-node triangles and compute the associated eigenvalues and the eigenfunctions.

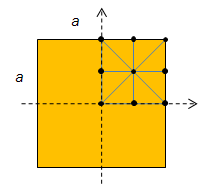
Note: Use a node numbering scheme that will make assembly of the stiffness and mass matrices as simple as possible.

As a check on your work, if you assume a = 1 and rw²/T = 1,then first two eigenvalues are 4.3889 and 33.6174.

The associated first two mode shapes are:

This web site was originally developed by Charles Camp for CIVL 7111.
This site is maintained by the Department of Civil Engineering at the University of Memphis.
Your comments and questions are welcomed.