Part 11 - Concrete as a Composite Material

A composite material may be defined as a combination of at least two chemically and mechanically distinct materials with a definite interface separating the components; clearly concrete qualifies. This definition of a composite works on many levels. At the macroscopic level. concrete consists of coarse aggregate embedded in a cement matrix; on a finer scale the mortar itself consists of sand embedded in a matrix of hydrated cement paste. On a microscopic level, the hydrated cement contains a network of capillary pores and grains of unhydrated cement. On a finer scale, the C-H-S is a mixture of poorly crystallized particles of varies shapes and a system of gel pores.

Factors Affecting Composite Behavior

Before a specific model for a composite can be formed, a number of parameters should be considered; (1) shape of the particles, (2) size and size distribution, (3) concentration and concentration distribution, (4) orientation of particles, (5) spatial distribution of particles, (6) composition of disperse phase, (7) composite of the continuous phase, and (8) bond between the continuous and disperse phases. Describing a system in terms of these parameters is very difficult. The purpose is to determine the elastic properties of the composite based on the properties of the components. The parallel system is the upper bound for elastic properties of interest while the series system provides the lower bound. For the parallel model, the modulus of elasticity can be determined as:

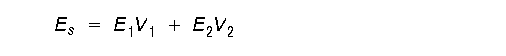
For a series model:

where Es is the modulus of elasticity of the system, E1, and E2 are the moduli of elasticity of the two components, and V1 and V2 are the volume fractions of the two components. These equations can be applied to concrete in the following forms:

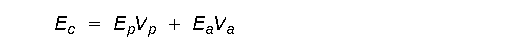
where Ec is the modulus of elasticity of concrete, Ep and Ea are the moduli of elasticity of the paste and the aggregate, and Vp and Va area the volume fractions of the paste and the aggregate.

Concrete made with natural aggregate in a soft paste conforms more closely to the lower bound, the series model. However, concrete made with lightweight aggregate in a hard matrix more closely resembles the parallel model. Another model suggested by Hirsch is expressed as:

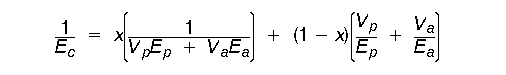
where x and 1-x are the relative proportions of material conforming to the upper and lower bound models. There is another model proposed by Counto.

A more realistic model is one consisting of spherical particles in a continuous matrix and can be expressed as:

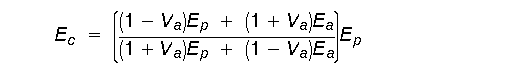
This model depends on the assumptions that (1) there is no interaction between the aggregate particles, and (2) that there is a perfect bond between aggregate and the matrix. The first assumption is valid; however, the second assumption is not.

For normal weight aggregates, the Ea is considerably higher than Ep, or the case of hard particles in a soft matrix; the theoretical lower limit. Therefore the true value for E should lie between the lower limit and the spherical model. If Ea = Ep for a lightweight concrete then Ec is independent of relative amounts of the cement and aggregate. For Ep > Ea, soft particles in a hard matrix, the modulus of elasticity is the upper limit.

Cement-Aggregate Bond

Concrete strength depends on the strength of the paste, the strength of the aggregate, and the strength of the paste-aggregate interface. The weakest region is the interface between the paste and the aggregate. This is affected by the shape and texture of the aggregate. The bond region is weak because cracks exist at the paste-coarse aggregate interface due to bleeding, segregation, volume change during hydration. Also, during curing, the aggregate helps resist shrinkage, which in turn induces shear and tensile forces at the aggregate surface.

• Factors Affecting Bond Strength -- Bond strength is very difficult to determine and there is no standard test. However, bond strength is reasonably well understood and there are several tests used to determine strength. Many of the same parameters that affect concrete strength also affect bond strength; e.g. w/c ratio, type of cement, and age. Vibration is important since air voids can reduce the contact surface. The potential for absorption capacity may be important; porous aggregate (dried before used) can produce an excellent bond. Bond failures do not occur between paste and fine aggregate. In fact, as particle size increases, the stress at the paste-aggregate interface increases.
  
  
• The shape and texture are also very important; a smooth texture can decrease (1) strength, (2) stress at which cracking begins, (3) total strain failure, (4) maximum volume strain, and (5) modulus of elasticity. A coarser surface should delay the onset of bond cracking. The shear bond strength is increased over the intrinsic shear strength due to frictional forces developed due to normal stresses.

Nature of Strength of Concrete

Concrete is a complex multiphase material where strength and mechanical properties are dependent on the interaction between the various components. Therefore, any discussion of strength is not absolute. In fact, a better approach to strength might be to explain why concrete is weak in tension rather than why it is strong in compression. In general, a normal weight aggregate is much more stiff than a cement paste, therefore the aggregate-paste bond is very important.

This website was originally developed by Charles Camp for his CIVL 1101 class.
This site is maintained by the Department of Civil Engineering at the University of Memphis.
Your comments and questions are more than welcome